Ensembles de nombres et leur représentation En mathématiques, nous distinguons divers ensembles de nombres:
* l'ensemble des entiers naturels IN,
* l'ensemble des entiers relatifs ZZ,
* l'ensemble des rationnels Q,
* l'ensemble des réels IR.
En mathématiques l'ordre de grandeur des nombres est illimité et les rationnels peuvent être exprimés sans perte de précision.
Un ordinateur ne peut traiter aisément que des nombres entiers d'une taille limitée. Il utilise le système binaire pour calculer et sauvegarder ces nombres. Ce n'est que par des astuces de calcul et de représentation que l'ordinateur obtient des valeurs correctement approchées des entiers très grands, des réels ou des rationnels à partie décimale infinie.
Les charges du programmeur
Même un programmeur utilisant C ne doit pas connaître tous les détails des méthodes de codage et de calcul, il doit quand même être capable de:
- choisir un type numérique approprié à un
problème donné;
c.-à-d.: trouver un optimum de
précision, de temps de calcul et d'espace à réserver en
mémoire
- choisir un type approprié pour la représentation sur l'écran
- prévoir le type résultant d'une opération entre
différents types numériques;
c.-à-d.:
connaître les transformations automatiques de type que C accomplit lors
des calculs (voir 3.7.1).
- prévoir et optimiser la précision des résultats
intermédiaires au cours d'un calcul complexe;
c.-à-d.:
changer si nécessaire l'ordre des opérations ou forcer
l'ordinateur à utiliser un type numérique mieux adapté
(casting: voir 3.7.2).
Exemple
![]()
Supposons que la mantisse du type choisi ne comprenne que 6 positions
décimales (ce qui est très réaliste pour le type
float):
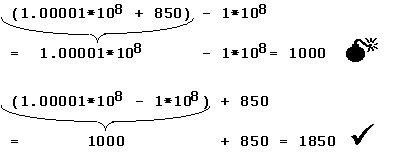
Retour Suite Index